Let's build a Neural Network with a few lines of code

In my previous post, I mentioned how to setup Python. Today I'm going to build a simple 2 Layer neural network using backpropagation. Let's start with the code. I prefer to understand the code before going for complicated theories and concepts. Because the other way round doesn't work for me. 😄

1. import numpy as la
2. from xlwings import xrange
4. # input data
5. X1 = la.array([[0, 0, 1], [1, 0, 1], [0, 1, 1]])
6. # output data
7. X2 = la.array([[0, 1, 0]]).T
9. # sigmoid function
10. def sigmoid(x, derivative=False):
11.     if (derivative == True):
12.         return x * (1 - x)
13.     return 1 / (1 + la.exp(-x))
15. # Generate random numbers
16. la.random.seed(1)
18. # initialize weights with mean 0
19. synapse0 = 2 * la.random.random((3, 1)) - 1
21. for iterations in xrange(10000):
22.     # forward propagation
23.     layer0 = X1
24.     layer1 = sigmoid(la.dot(layer0, synapse0))
26.     # error calculation
27.     layer1_error = X2 - layer1
29.     # multiply slopes by the error
30.     # (reduce the error of high confidence predictions)
31.     layer1_delta = layer1_error * sigmoid(layer1, True)
33.     # weight update
34.     synapse0 += la.dot(layer0.T, layer1_delta)
36. print("Trained output:")
37. print(layer1)

The above code will give the below output.

Trained output: [[ 0.01225605]  [ 0.98980175]  [ 0.0024512 ]]

The following table contains the input dataset and output dataset which the neural network was based on. As you can see, the highlighted input column is correlated with the output column. What we are trying to do here is, create a model to predict the output with the given input.

Input			Output
0	0	1	0
1	0	1	1
0	1	1	0

We can see the following characteristics when building a neural network using backpropagation.

• Assign random weights while initializing the network
• Provide input data to the network and calculate the output
• Compute the error by comparing the network output and correct output(error function) 
• Propagate the error term back to the previous layer and update the weights and then repeat this until the error stops improving

Let's try to understand the code.

1. import numpy as la

Numpy is a scientific computing library in Python. It contains useful linear algebra, Fourier transform, N-dimensional array objects etc. In this example, we use it for arrays and random number generations.


5. X1 = la.array([[0, 0, 1], [1, 0, 1], [0, 1, 1]])

6. X2 = la.array([[0, 1, 0]]).T

In lines 5&6, we assign the arrays of input and output to X1 and X2 respectively. We take transpose (T) of the output dataset to match with the input. Because input is a 3x3 matrix and we need to obtain the 3x1 matrix of output.

10. def sigmoid(x, derivative=False):
11.    if (derivative == True):
12.        return x * (1 - x)
14.    return 1 / (1 + la.exp(-x))

In backpropagation we need proper activation function to activate the hidden unit. The activation function should be continuous, easy to compute, non decreasing and non differential.  Sigmoid function satisfies almost all the conditions. Sigmoid function go either from 0 to 1 or from -1 to 1 based on the convention. In here, we use values between 0 and 1 for converting numbers to probabilities.

We use the first derivative of the Sigmoid function to calculate the gradient since it is very convenient. If you are not good with derivatives, refer tutorials. 

16. la.random.seed(1)

This line generates random numbers for the calculation.

19. synapse0 = 2 * la.random.random((3, 1)) - 1

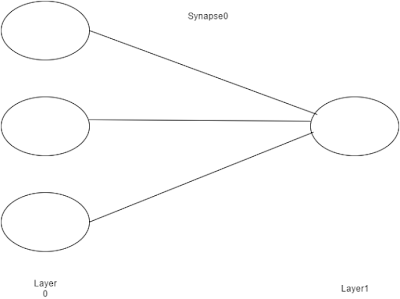
In real world, synapse assist in passing electrical or chemical signal between the neurons. There is no much difference in machine learning, we use synapse as a matrix of weights to connect input layer with the output layer. In this scenario we have only two layers therefore we need only one matrix of weights. It's a 3x1 matrix since we have three inputs and one output.

In this line, weights will be initialized with mean zero. Because initially system is unsure of the weights. However as the system learns, it becomes sure of it's output probabilities.

21. for iterations in xrange(10000):

In our code, training starts from here. The xrange() function generates list of integers. This loop iterates for several times to optimize our network to the given datasets.

24. layer1 = sigmoid(la.dot(layer0, synapse0))

In this step the network predict output for the given input. The synapse0 matrix will be multiplied by the layer0 matrix and will be sent to the Sigmoid function.



Then the network will provide 3 output guesses for the given input.


27. layer1_error = X2 - layer1

In this line, it calculates how much the guessed output deviated from the correct output.



31. layer1_delta = layer1_error * sigmoid(layer1, True)

This is the most important code line. If we reconsider the Sigmoid diagram, you can see that it has shallow slope when it comes to high positive/negative values. And the steepest slope will be at zero. If the network guessed high positive/negative values for some output that means it is quite confident about the result. Therefore those values will be multiplied by the values which are closer to zero in order to reduce the effect. And if  some values are closer to zero, it means that network is not much confident about these values. Then those values should be heavily updated.

The network use the three input training sets at the same time which is called "full batch configuration". However to explain the scenario I'll use just one training example.

In this instance, the top weight will be updated slightly. It is because the network is already confident with the value.

You can debug the code and check how this really works, it's quite amazing. 😊

Now you can check the result for simple AND truth table and think why you got such a result.

Hope to go deeper into the neural networks with my next post. Let's see 😜